This post was originally published over at jooq.org, a blog focusing on all things open source, Java and software development from the perspective of jOOQ.
Listicles like these do work – not only do they attract attention, if the content is also valuable (and in this case it is, trust me), the article format can be extremely entertaining.
This article will bring you 10 SQL tricks that many of you might not have thought were possible. The article is a summary of my new, extremely fast-paced, ridiculously childish-humored talk, which I’m giving at conferences (recently at JAX). You may quote me on this:
Last minute slide added to my ridiculously fast paced SQL talk at @JAXconf, the talk you mustn’t miss #Microservicespic.twitter.com/leHuxuolK6
— Lukas Eder (@lukaseder) April 20, 2016
The full slides can be seen on SlideShare:
Introduction
From early days onwards, programming language designers had this desire to design languages in which you tell the machine WHAT you want as a result, not HOW to obtain it. For instance, in SQL, you tell the machine that you want to “connect” (JOIN) the user table and the address table and find the users that live in Switzerland. You don’t care HOW the database will retrieve this information (e.g. should the users table be loaded first, or the address table? Should the two tables be joined in a nested loop or with a hashmap? Should all data be loaded in memory first and then filtered for Swiss users, or should we only load Swiss addresses in the first place? Etc.)
As with every abstraction, you will still need to know the basics of what’s going on behind the scenes in a database to help the database make the right decisions when you query it. For instance, it makes sense to:
- Establish a formal foreign key relationship between the tables (this tells the database that every address is guaranteed to have a corresponding user)
- Add an index on the search field: The country (this tells the database that specific countries can be found in
O(log N)instead ofO(N))
But once your database and your application matures, you will have put all the important meta data in place and you can focus on your business logic only. The following 10 tricks show amazing functionality written in only a few lines of declarative SQL, producing simple and also complex output.
1. Everything is a Table
This is the most trivial of tricks, and not even really a trick, but it is fundamental to a thorough understanding of SQL: Everything is a table! When you see a SQL statement like this:
SELECT * FROM person
… you will quickly spot the table person sitting right there in the FROM clause. That’s cool, that is a table. But did you realize that the whole statement is also a table? For instance, you can write:
SELECT * FROM ( SELECT * FROM person ) t
And now, you have created what is called a “derived table” – i.e. a nestedSELECT statement in a FROM clause.
That’s trivial, but if you think of it, quite elegant. You can also create ad-hoc, in-memory tables with the VALUES() constructor as such, in some databases (e.g. PostgreSQL, SQL Server):
SELECT * FROM ( VALUES(1),(2),(3) ) t(a)
Which simply yields:
a
—
1
2
3
If that clause is not supported, you can revert to derived tables, e.g. in Oracle:
SELECT * FROM ( SELECT 1 AS a FROM DUAL UNION ALL SELECT 2 AS a FROM DUAL UNION ALL SELECT 3 AS a FROM DUAL ) t
Now that you’re seeing that VALUES() and derived tables are really the same thing, conceptually, let’s review the INSERT statement, which comes in two flavors:
-- SQL Server, PostgreSQL, some others: INSERT INTO my_table(a) VALUES(1),(2),(3); -- Oracle, many others: INSERT INTO my_table(a) SELECT 1 AS a FROM DUAL UNION ALL SELECT 2 AS a FROM DUAL UNION ALL SELECT 3 AS a FROM DUAL
In SQL everything is a table. When you’re inserting rows into a table, you’re not really inserting individual rows. You’re really inserting entire tables. Most people just happen to insert a single-row-table most of the time, and thus don’t realize what INSERT really does.
Everything is a table. In PostgreSQL, even functions are tables:
SELECT *
FROM substring('abcde', 2, 3)
The above yields:
substring
———
bcd
If you’re programming in Java, you can use the analogy of the Java 8 Stream API to take this one step further. Consider the following equivalent concepts:
TABLE : Stream<Tuple<..>> SELECT : map() DISTINCT : distinct() JOIN : flatMap() WHERE / HAVING : filter() GROUP BY : collect() ORDER BY : sorted() UNION ALL : concat()
With Java 8, “everything is a Stream” (as soon as you start working with Streams, at least). No matter how you transform a stream, e.g. with map() or filter(), the resulting type is always a Stream again.
We’ve written an entire article to explain this more deeply, and to compare the Stream API with SQL:
Common SQL Clauses and Their Equivalents in Java 8 Streams
And if you’re looking for “better streams” (i.e. streams with even more SQL semantics), do check out jOOλ, an open source library that brings SQL window functions to Java.
2. Data generation with recursive SQL
Common Table Expressions (also: CTE, also referred to as subquery factoring, e.g. in Oracle) are the only way to declare variables in SQL (apart from the obscure WINDOW clause that only PostgreSQL and Sybase SQL Anywhere know).
This is a powerful concept. Extremely powerful. Consider the following statement:
-- Table variables
WITH
t1(v1, v2) AS (SELECT 1, 2),
t2(w1, w2) AS (
SELECT v1 * 2, v2 * 2
FROM t1
)
SELECT *
FROM t1, t2
It yields
v1 v2 w1 w2 ----------------- 1 2 2 4
Using the simple WITH clause, you can specify a list of table variables (remember: everything is a table), which may even depend on each other.
That is easy to understand. This makes CTE (Common Table Expressions) already very useful, but what’s really really awesome is that they’re allowed to be recursive! Consider the following PostgreSQL example:
WITH RECURSIVE t(v) AS ( SELECT 1 -- Seed Row UNION ALL SELECT v + 1 -- Recursion FROM t ) SELECT v FROM t LIMIT 5
It yields
—
1
2
3
4
5
How does it work? It’s relatively easy, once you see through the many keywords. You define a common table expression that has exactly two UNION ALL subqueries.
The first UNION ALL subquery is what I usually call the “seed row”. It “seeds” (initialises) the recursion. It can produce one or several rows on which we will recurse afterwards. Remember: everything is a table, so our recursion will happen on a whole table, not on an individual row/value.
The second UNION ALL subquery is where the recursion happens. If you look closely, you will observe that it selects from t. I.e. the second subquery is allowed to select from the very CTE that we’re about to declare. Recursively. It thus has also access to the column v, which is being declared by the CTE that already uses it.
In our example, we seed the recursion with the row (1), and then recurse by adding v + 1. The recursion is then stopped at the use-site by setting aLIMIT 5 (beware of potentially infinite recursions – just like with Java 8 Streams).
Side note: Turing completeness
Recursive CTE make SQL:1999 turing complete, which means that any program can be written in SQL! (if you’re crazy enough)
One impressive example that frequently shows up on blogs: The Mandelbrot Set, e.g. as displayed on http://explainextended.com/2013/12/31/happy-new-year-5/
WITH RECURSIVE q(r, i, rx, ix, g) AS (
SELECT r::DOUBLE PRECISION * 0.02, i::DOUBLE PRECISION * 0.02,
.0::DOUBLE PRECISION , .0::DOUBLE PRECISION, 0
FROM generate_series(-60, 20) r, generate_series(-50, 50) i
UNION ALL
SELECT r, i, CASE WHEN abs(rx * rx + ix * ix) &amp;lt;= 2 THEN rx * rx - ix * ix END + r,
CASE WHEN abs(rx * rx + ix * ix) &amp;lt;= 2 THEN 2 * rx * ix END + i, g + 1
FROM q
WHERE rx IS NOT NULL AND g &amp;lt; 99
)
SELECT array_to_string(array_agg(s ORDER BY r), '')
FROM (
SELECT i, r, substring(' .:-=+*#%@', max(g) / 10 + 1, 1) s
FROM q
GROUP BY i, r
) q
GROUP BY i
ORDER BY i
Run the above on PostgreSQL, and you’ll get something like
.-.:-.......==..*.=.::-@@@@@:::.:.@..*-. =.
...=...=...::+%.@:@@@@@@@@@@@@@+*#=.=:+-. ..-
.:.:=::*....@@@@@@@@@@@@@@@@@@@@@@@@=@@.....::...:.
...*@@@@=.@:@@@@@@@@@@@@@@@@@@@@@@@@@@=.=....:...::.
.::@@@@@:-@@@@@@@@@@@@@@@@@@@@@@@@@@@@:@..-:@=*:::.
.-@@@@@-@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@.=@@@@=..:
...@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@:@@@@@:..
....:-*@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@::
.....@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@-..
.....@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@-:...
.--:+.@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@...
.==@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@-..
..+@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@-#.
...=+@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@..
-.=-@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@..:
.*%:@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@:@-
. ..:... ..-@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
.............. ....-@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@%@=
.--.-.....-=.:..........::@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@..
..=:-....=@+..=.........@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@:.
.:+@@::@==@-*:%:+.......:@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@.
::@@@-@@@@@@@@@-:=.....:@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@:
.:@@@@@@@@@@@@@@@=:.....%@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
.:@@@@@@@@@@@@@@@@@-...:@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@:-
:@@@@@@@@@@@@@@@@@@@-..%@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@.
%@@@@@@@@@@@@@@@@@@@-..-@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@.
@@@@@@@@@@@@@@@@@@@@@::+@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@+
@@@@@@@@@@@@@@@@@@@@@@:@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@..
@@@@@@@@@@@@@@@@@@@@@@-@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@-
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@.
Impressive, huh?
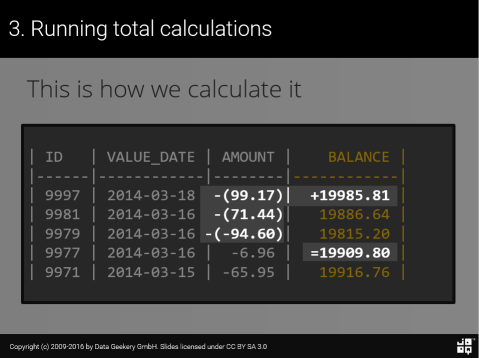
3. Running Total Calculations
This blog is full of running total examples. They’re some of the most educational examples to learn about advanced SQL, because there are at least a dozen of ways how to implement a running total.
A running total is easy to understand, conceptually.
In Microsoft Excel, you would simply calculate a sum (or difference) of two previous (or subsequent) values, and then use the useful crosshair cursor to pull that formula through your entire spreadsheet. You “run” that total through the spreadsheet. A “running total”.
In SQL, the best way to do that is by using window functions, another topic that this blog has covered many many times.
Window functions are a powerful concept – not so easy to understand at first, but in fact, they’re really really easy:
Window functions are aggregations / rankings on a subset of rows relative to the current row being transformed by SELECT
That’s it.
What it essentially means is that a window function can perform calculations on rows that are “above” or “below” the current row. Unlike ordinary aggregations and GROUP BY, however, they don’t transform the rows, which makes them very useful.
The syntax can be summarized as follows, with individual parts being optional
function(...) OVER ( PARTITION BY ... ORDER BY ... ROWS BETWEEN ... AND ... )
So, we have any sort of function (we’ll see examples for such functions later), followed by this OVER() clause, which specifies the window. I.e. this OVER()clause defines:
- The
PARTITION: Only rows that are in the same partition as the current row will be considered for the window - The
ORDER: The window can be ordered independently of what we’re selecting - The
ROWS(orRANGE) frame definition: The window can be restricted to a fixed amount of rows “ahead” and “behind”
That’s all there is to window functions.
Now how does that help us calculate a running total? Consider the following data:
| ID | VALUE_DATE | AMOUNT | BALANCE | |------|------------|--------|------------| | 9997 | 2014-03-18 | 99.17 | 19985.81 | | 9981 | 2014-03-16 | 71.44 | 19886.64 | | 9979 | 2014-03-16 | -94.60 | 19815.20 | | 9977 | 2014-03-16 | -6.96 | 19909.80 | | 9971 | 2014-03-15 | -65.95 | 19916.76 |
Let’s assume that BALANCE is what we want to calculate from AMOUNT
Intuitively, we can immediately see that the following holds true:
So, in plain English, any balance can be expressed with the following pseudo SQL:
“all the rows on top of the current row”
)
In real SQL, that would then be written as follows:
SUM(t.amount) OVER (
PARTITION BY t.account_id
ORDER BY t.value_date DESC,
t.id DESC
ROWS BETWEEN UNBOUNDED PRECEDING
AND 1 PRECEDING
)
Explanation:
- The partition will calculate the sum for each bank account, not for the entire data set
- The ordering will guarantee that transactions are ordered (within the partition) prior to summing
- The rows clause will consider only preceding rows (within the partition, given the ordering) prior to summing
All of this will happen in-memory over the data set that has already been selected by you in your FROM .. WHERE etc. clauses, and is thus extremely fast.
Intermezzo
Before we move on to all the other awesome tricks, consider this: We’ve seen
- (Recursive) Common Table Expressions (CTE)
- Window functions
Both of these features are:
- Awesome
- Exremely powerful
- Declarative
- Part of the SQL standard
- Available in most popular RDBMS (except MySQL)
- Very important building blocks
If anything can be concluded from this article, it is the fact that you should absolutely know these two building blocks of modern SQL. Why? Because:
4. Finding the largest series with no gaps
Stack Overflow has this very nice feature to motivate people to stay on their website for as long as possible. Badges:
For scale, you can see how many badges I have. Tons.
How do you calculate these badges? Let’s have a look at the “Enthusiast” and the “Fanatic”. These badges are awarded to anyone who spends a given amount of consecutive days on their platform. Regardless of any wedding date or wife’s birthday, you HAVE TO LOG IN, or the counter starts from zero again.
Now as we’re doing declarative programming, we don’t care about maintaining any state and in-memory counters. We want to express this in the form of online analytic SQL. I.e. consider this data:
| LOGIN_TIME | |---------------------| | 2014-03-18 05:37:13 | | 2014-03-16 08:31:47 | | 2014-03-16 06:11:17 | | 2014-03-16 05:59:33 | | 2014-03-15 11:17:28 | | 2014-03-15 10:00:11 | | 2014-03-15 07:45:27 | | 2014-03-15 07:42:19 | | 2014-03-14 09:38:12 |
That doesn’t help much. Let’s remove the hours from the timestamp. That’s easy:
SELECT DISTINCT cast(login_time AS DATE) AS login_date FROM logins WHERE user_id = :user_id
Which yields:
| LOGIN_DATE | |------------| | 2014-03-18 | | 2014-03-16 | | 2014-03-15 | | 2014-03-14 |
Now, that we’ve learned about window functions, let’s just add a simple row number to each of these dates:
SELECT login_date, row_number() OVER (ORDER BY login_date) FROM login_dates
Which produces:
| LOGIN_DATE | RN | |------------|----| | 2014-03-18 | 4 | | 2014-03-16 | 3 | | 2014-03-15 | 2 | | 2014-03-14 | 1 |
Still easy. Now, what happens, if instead of selecting these values separately, we subtract them?
SELECT login_date - row_number() OVER (ORDER BY login_date) FROM login_dates
We’re getting something like this:
| LOGIN_DATE | RN | GRP | |------------|----|------------| | 2014-03-18 | 4 | 2014-03-14 | | 2014-03-16 | 3 | 2014-03-13 | | 2014-03-15 | 2 | 2014-03-13 | | 2014-03-14 | 1 | 2014-03-13 |
Wow. Interesting. So, 14 – 1 = 13, 15 – 2 = 13, 16 – 3 = 13, but 18 – 4 = 14. No one can say it better than Doge:
There’s a simple example for this behavior:
- ROW_NUMBER() never has gaps. That’s how it’s defined
- Our data, however, does
So when we subtract a “gapless” series of consecutive integers from a “gapful” series of non-consecutive dates, we will get the same date for each “gapless” subseries of consecutive dates, and we’ll get a new date again where the date series had gaps.
Huh.
This means we can now simply GROUP BY this arbitrary date value:
SELECT min(login_date), max(login_date), max(login_date) - min(login_date) + 1 AS length FROM login_date_groups GROUP BY grp ORDER BY length DESC
And we’re done. The largest series of consecutive dates with no gaps has been found:
| MIN | MAX | LENGTH | |------------|------------|--------| | 2014-03-14 | 2014-03-16 | 3 | | 2014-03-18 | 2014-03-18 | 1 |
With the full query being:
WITH
login_dates AS (
SELECT DISTINCT cast(login_time AS DATE) login_date
FROM logins WHERE user_id = :user_id
),
login_date_groups AS (
SELECT
login_date,
login_date - row_number() OVER (ORDER BY login_date) AS grp
FROM login_dates
)
SELECT
min(login_date), max(login_date),
max(login_date) - min(login_date) + 1 AS length
FROM login_date_groups
GROUP BY grp
ORDER BY length DESC
Not that hard in the end, right? Of course, having the idea makes all the difference, but the query itself is really very very simple and elegant. No way you could implement some imperative-style algorithm in a leaner way than this.
Whew.
5. Finding the Length of a Series
Previously, we had seen series of consecutive values. That’s easy to deal with as we can abuse of the consecutiveness of integers. What if the definition of a “series” is less intuitive, and in addition to that, several series contain the same values? Consider the following data, where LENGTH is the length of each series that we want to calculate:
| ID | VALUE_DATE | AMOUNT | LENGTH | |------|------------|--------|------------| | 9997 | 2014-03-18 | 99.17 | 2 | | 9981 | 2014-03-16 | 71.44 | 2 | | 9979 | 2014-03-16 | -94.60 | 3 | | 9977 | 2014-03-16 | -6.96 | 3 | | 9971 | 2014-03-15 | -65.95 | 3 | | 9964 | 2014-03-15 | 15.13 | 2 | | 9962 | 2014-03-15 | 17.47 | 2 | | 9960 | 2014-03-15 | -3.55 | 1 | | 9959 | 2014-03-14 | 32.00 | 1 |
Yes, you’ve guessed right. A “series” is defined by the fact that consecutive (ordered by ID) rows have the same SIGN(AMOUNT). Check again the data formatted as below:
| ID | VALUE_DATE | AMOUNT | LENGTH | |------|------------|--------|------------| | 9997 | 2014-03-18 | +99.17 | 2 | | 9981 | 2014-03-16 | +71.44 | 2 | | 9979 | 2014-03-16 | -94.60 | 3 | | 9977 | 2014-03-16 | - 6.96 | 3 | | 9971 | 2014-03-15 | -65.95 | 3 | | 9964 | 2014-03-15 | +15.13 | 2 | | 9962 | 2014-03-15 | +17.47 | 2 | | 9960 | 2014-03-15 | - 3.55 | 1 | | 9959 | 2014-03-14 | +32.00 | 1 |
How do we do it? “Easy” First, let’s get rid of all the noise, and add another row number:
SELECT
id, amount,
sign(amount) AS sign,
row_number()
OVER (ORDER BY id DESC) AS rn
FROM trx
This will give us:
| ID | AMOUNT | SIGN | RN | |------|--------|------|----| | 9997 | 99.17 | 1 | 1 | | 9981 | 71.44 | 1 | 2 | | 9979 | -94.60 | -1 | 3 | | 9977 | -6.96 | -1 | 4 | | 9971 | -65.95 | -1 | 5 | | 9964 | 15.13 | 1 | 6 | | 9962 | 17.47 | 1 | 7 | | 9960 | -3.55 | -1 | 8 | | 9959 | 32.00 | 1 | 9 |
Now, the next goal is to produce the following table:
| ID | AMOUNT | SIGN | RN | LO | HI | |------|--------|------|----|----|----| | 9997 | 99.17 | 1 | 1 | 1 | | | 9981 | 71.44 | 1 | 2 | | 2 | | 9979 | -94.60 | -1 | 3 | 3 | | | 9977 | -6.96 | -1 | 4 | | | | 9971 | -65.95 | -1 | 5 | | 5 | | 9964 | 15.13 | 1 | 6 | 6 | | | 9962 | 17.47 | 1 | 7 | | 7 | | 9960 | -3.55 | -1 | 8 | 8 | 8 | | 9959 | 32.00 | 1 | 9 | 9 | 9 |
In this table, we want to copy the row number value into “LO” at the “lower” end of a series, and into “HI” at the “upper” end of a series. For this we’ll be using the magical LEAD() and LAG(). LEAD() can access the n-th next row from the current row, whereas LAG() can access the n-th previous row from the current row. For example:
SELECT lag(v) OVER (ORDER BY v), v, lead(v) OVER (ORDER BY v) FROM ( VALUES (1), (2), (3), (4) ) t(v)
The above query produces:
That’s awesome! Remember, with window functions, you can perform rankings or aggregations on a subset of rows relative to the current row. In the case of LEAD() and LAG(), we simply access a single row relative to the current row, given its offset. This is useful in so many cases.
Continuing with our “LO” and “HI” example, we can simply write:
SELECT
trx.*,
CASE WHEN lag(sign)
OVER (ORDER BY id DESC) != sign
THEN rn END AS lo,
CASE WHEN lead(sign)
OVER (ORDER BY id DESC) != sign
THEN rn END AS hi,
FROM trx
… in which we compare the “previous” sign (lag(sign)) with the “current” sign (sign). If they’re different, we put the row number in “LO”, because that’s the lower bound of our series.
Then we compare the “next” sign (lead(sign)) with the “current” sign (sign). If they’re different, we put the row number in “HI”, because that’s the upper bound of our series.
Finally, a little boring NULL handling to get everything right, and we’re done:
SELECT -- With NULL handling...
trx.*,
CASE WHEN coalesce(lag(sign)
OVER (ORDER BY id DESC), 0) != sign
THEN rn END AS lo,
CASE WHEN coalesce(lead(sign)
OVER (ORDER BY id DESC), 0) != sign
THEN rn END AS hi,
FROM trx
Next step. We want “LO” and “HI” to appear in ALL rows, not just at the “lower” and “upper” bounds of a series. E.g. like this:
| ID | AMOUNT | SIGN | RN | LO | HI | |------|--------|------|----|----|----| | 9997 | 99.17 | 1 | 1 | 1 | 2 | | 9981 | 71.44 | 1 | 2 | 1 | 2 | | 9979 | -94.60 | -1 | 3 | 3 | 5 | | 9977 | -6.96 | -1 | 4 | 3 | 5 | | 9971 | -65.95 | -1 | 5 | 3 | 5 | | 9964 | 15.13 | 1 | 6 | 6 | 7 | | 9962 | 17.47 | 1 | 7 | 6 | 7 | | 9960 | -3.55 | -1 | 8 | 8 | 8 | | 9959 | 32.00 | 1 | 9 | 9 | 9 |
We’re using a feature that is available at least in Redshift, Sybase SQL Anywhere, DB2, Oracle. We’re using the “IGNORE NULLS” clause that can be passed to some window functions:
SELECT
trx.*,
last_value (lo) IGNORE NULLS OVER (
ORDER BY id DESC
ROWS BETWEEN UNBOUNDED PRECEDING
AND CURRENT ROW) AS lo,
first_value(hi) IGNORE NULLS OVER (
ORDER BY id DESC
ROWS BETWEEN CURRENT ROW
AND UNBOUNDED FOLLOWING) AS hi
FROM trx
A lot of keywords! But the essence is always the same. From any given “current” row, we look at all the “previous values” (ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW), but ignoring all the nulls. From those previous values, we take the last value, and that’s our new “LO” value. In other words, we take the “closest preceding” “LO” value.
The same with “HI”. From any given “current” row, we look at all the “subsequent values” (ROWS BETWEEN CURRENT ROW AND UNBOUNDED FOLLOWING), but ignoring all the nulls. From the subsequent values, we take the first value, and that’s our new “HI” value. In other words, we take the “closest following” “HI” value.
Explained in Powerpoint:
Getting it 100% correct, with a little boring NULL fiddling:
SELECT -- With NULL handling...
trx.*,
coalesce(last_value (lo) IGNORE NULLS OVER (
ORDER BY id DESC
ROWS BETWEEN UNBOUNDED PRECEDING
AND CURRENT ROW), rn) AS lo,
coalesce(first_value(hi) IGNORE NULLS OVER (
ORDER BY id DESC
ROWS BETWEEN CURRENT ROW
AND UNBOUNDED FOLLOWING), rn) AS hi
FROM trx
Finally, we’re just doing a trivial last step, keeping in mind off-by-1 errors:
SELECT trx.*, 1 + hi - lo AS length FROM trx
And we’re done. Here’s our result:
| ID | AMOUNT | SIGN | RN | LO | HI | LENGTH| |------|--------|------|----|----|----|-------| | 9997 | 99.17 | 1 | 1 | 1 | 2 | 2 | | 9981 | 71.44 | 1 | 2 | 1 | 2 | 2 | | 9979 | -94.60 | -1 | 3 | 3 | 5 | 3 | | 9977 | -6.96 | -1 | 4 | 3 | 5 | 3 | | 9971 | -65.95 | -1 | 5 | 3 | 5 | 3 | | 9964 | 15.13 | 1 | 6 | 6 | 7 | 2 | | 9962 | 17.47 | 1 | 7 | 6 | 7 | 2 | | 9960 | -3.55 | -1 | 8 | 8 | 8 | 1 | | 9959 | 32.00 | 1 | 9 | 9 | 9 | 1 |
And the full query here:
WITH
trx1(id, amount, sign, rn) AS (
SELECT id, amount, sign(amount), row_number() OVER (ORDER BY id DESC)
FROM trx
),
trx2(id, amount, sign, rn, lo, hi) AS (
SELECT trx1.*,
CASE WHEN coalesce(lag(sign) OVER (ORDER BY id DESC), 0) != sign
THEN rn END,
CASE WHEN coalesce(lead(sign) OVER (ORDER BY id DESC), 0) != sign
THEN rn END
FROM trx1
)
SELECT
trx2.*, 1
- last_value (lo) IGNORE NULLS OVER (ORDER BY id DESC
ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW)
+ first_value(hi) IGNORE NULLS OVER (ORDER BY id DESC
ROWS BETWEEN CURRENT ROW AND UNBOUNDED FOLLOWING)
FROM trx2
Huh. This SQL thing does start getting interesting!
Ready for more?
6. The subset sum problem with SQL
This is my favourite!
What is the subset sum problem? Find a fun explanation here:
https://xkcd.com/287
And a boring one here:
https://en.wikipedia.org/wiki/Subset_sum_problem
Essentially, for each of these totals…
| ID | TOTAL | |----|-------| | 1 | 25150 | | 2 | 19800 | | 3 | 27511 |
… we want to find the “best” (i.e. the closest) sum possible, consisting of any combination of these items:
| ID | ITEM | |------|-------| | 1 | 7120 | | 2 | 8150 | | 3 | 8255 | | 4 | 9051 | | 5 | 1220 | | 6 | 12515 | | 7 | 13555 | | 8 | 5221 | | 9 | 812 | | 10 | 6562 |
As you’re all quick with your mental mathemagic processing, you have immediately calculated these to be the best sums:
| TOTAL | BEST | CALCULATION |-------|-------|-------------------------------- | 25150 | 25133 | 7120 + 8150 + 9051 + 812 | 19800 | 19768 | 1220 + 12515 + 5221 + 812 | 27511 | 27488 | 8150 + 8255 + 9051 + 1220 + 812
How to do it with SQL? Easy. Just create a CTE that contains all the 2n *possible* sums and then find the closest one for each TOTAL:
-- All the possible 2N sums WITH sums(sum, max_id, calc) AS (...) -- Find the best sum per “TOTAL” SELECT totals.total, something_something(total - sum) AS best, something_something(total - sum) AS calc FROM draw_the_rest_of_the_*bleep*_owl
As you’re reading this, you might be like my friend here:
But don’t worry, the solution is – again – not all that hard (although it doesn’t perform due to the nature of the algorithm):
WITH sums(sum, id, calc) AS (
SELECT item, id, to_char(item) FROM items
UNION ALL
SELECT item + sum, items.id, calc || ' + ' || item
FROM sums JOIN items ON sums.id < items.id
)
SELECT
totals.id,
totals.total,
min (sum) KEEP (
DENSE_RANK FIRST ORDER BY abs(total - sum)
) AS best,
min (calc) KEEP (
DENSE_RANK FIRST ORDER BY abs(total - sum)
) AS calc,
FROM totals
CROSS JOIN sums
GROUP BY totals.id, totals.total
In this article, I won’t explain the details of this solution, because the example has been taken from a previous article that you can find here:
How to find the closest subset sum with SQL
Enjoy reading the details, but be sure to come back here for the remaining 4 tricks:
7. Capping a Running Total
So far, we’ve seen how to calculate an “ordinary” running total with SQL using window functions. That was easy. Now, how about if we cap the running total such that it never goes below zero? Essentially, we want to calculate this:
| DATE | AMOUNT | TOTAL | |------------|--------|-------| | 2012-01-01 | 800 | 800 | | 2012-02-01 | 1900 | 2700 | | 2012-03-01 | 1750 | 4450 | | 2012-04-01 | -20000 | 0 | | 2012-05-01 | 900 | 900 | | 2012-06-01 | 3900 | 4800 | | 2012-07-01 | -2600 | 2200 | | 2012-08-01 | -2600 | 0 | | 2012-09-01 | 2100 | 2100 | | 2012-10-01 | -2400 | 0 | | 2012-11-01 | 1100 | 1100 | | 2012-12-01 | 1300 | 2400 |
So, when that big negative AMOUNT -20000 was subtracted, instead of displaying the real TOTAL of -15550, we simply display 0. In other words (or data sets):
| DATE | AMOUNT | TOTAL | |------------|--------|-------| | 2012-01-01 | 800 | 800 | GREATEST(0, 800) | 2012-02-01 | 1900 | 2700 | GREATEST(0, 2700) | 2012-03-01 | 1750 | 4450 | GREATEST(0, 4450) | 2012-04-01 | -20000 | 0 | GREATEST(0, -15550) | 2012-05-01 | 900 | 900 | GREATEST(0, 900) | 2012-06-01 | 3900 | 4800 | GREATEST(0, 4800) | 2012-07-01 | -2600 | 2200 | GREATEST(0, 2200) | 2012-08-01 | -2600 | 0 | GREATEST(0, -400) | 2012-09-01 | 2100 | 2100 | GREATEST(0, 2100) | 2012-10-01 | -2400 | 0 | GREATEST(0, -300) | 2012-11-01 | 1100 | 1100 | GREATEST(0, 1100) | 2012-12-01 | 1300 | 2400 | GREATEST(0, 2400)
How will we do it?
Exactly. With obscure, vendor-specific SQL. In this case, we’re using Oracle SQL
How does it work? Surprisingly easy!
Just add MODEL after any table, and you’re opening up a can of awesome SQL worms!
SELECT ... FROM some_table -- Put this after any table MODEL ...
Once we put MODEL there, we can implement spreadsheet logic directly in our SQL statements, just as with Microsoft Excel.
The following three clauses are the most useful and widely used (i.e. 1-2 per year by anyone on this planet):
MODEL -- The spreadsheet dimensions DIMENSION BY ... -- The spreadsheet cell type MEASURES ... -- The spreadsheet formulas RULES ...
The meaning of each of these three additional clauses is best explained with slides again.
The DIMENSION BY clause specifies the dimensions of your spreadsheet. Unlike in MS Excel, you can have any number of dimensions in Oracle:
The MEASURES clause specifies the values that are available in each cell of your spreadsheet. Unlike in MS Excel, you can have a whole tuple in each cell in Oracle, not just a single value.
The RULES clause specifies the formulas that apply to each cell in your spreadsheet. Unlike in MS Excel, these rules / formulas are centralized at a single place, instead of being put inside of each cell:
This design makes MODEL a bit harder to use than MS Excel, but much more powerful, if you dare. The whole query will then be “trivially”:
SELECT *
FROM (
SELECT date, amount, 0 AS total
FROM amounts
)
MODEL
DIMENSION BY (row_number() OVER (ORDER BY date) AS rn)
MEASURES (date, amount, total)
RULES (
total[any] = greatest(0,
coalesce(total[cv(rn) - 1], 0) + amount[cv(rn)])
)
This whole thing is so powerful, it ships with its own white paper by Oracle, so rather than explaining things further here in this article, please do read the excellent white paper:
http://www.oracle.com/technetwork/middleware/bi-foundation/10gr1-twp-bi-dw-sqlmodel-131067.pdf
8. Time Series Pattern Recognition
If you’re into fraud detection or any other field that runs real time analytics on large data sets, time series pattern recognition is certainly not a new term to you.
If we review the “length of a series” data set, we might want to generate triggers on complex events over our time series as such:
| ID | VALUE_DATE | AMOUNT | LEN | TRIGGER |------|------------|---------|-----|-------- | 9997 | 2014-03-18 | + 99.17 | 1 | | 9981 | 2014-03-16 | - 71.44 | 4 | | 9979 | 2014-03-16 | - 94.60 | 4 | x | 9977 | 2014-03-16 | - 6.96 | 4 | | 9971 | 2014-03-15 | - 65.95 | 4 | | 9964 | 2014-03-15 | + 15.13 | 3 | | 9962 | 2014-03-15 | + 17.47 | 3 | | 9960 | 2014-03-15 | + 3.55 | 3 | | 9959 | 2014-03-14 | - 32.00 | 1 |
The rule of the above trigger is:
Trigger on the 3rd repetition of an event if the event occurs more than 3 times.
Similar to the previous MODEL clause, we can do this with an Oracle-specific clause that was added to Oracle 12c:
SELECT ... FROM some_table -- Put this after any table to pattern-match -- the table’s contents MATCH_RECOGNIZE (...)
The simplest possible application of MATCH_RECOGNIZE includes the following subclauses:
SELECT * FROM series MATCH_RECOGNIZE ( -- Pattern matching is done in this order ORDER BY ... -- These are the columns produced by matches MEASURES ... -- A short specification of what rows are -- returned from each match ALL ROWS PER MATCH -- «Regular expressions» of events to match PATTERN (...) -- The definitions of «what is an event» DEFINE ... )
That sounds crazy. Let’s look at some example clause implementations
SELECT *
FROM series
MATCH_RECOGNIZE (
ORDER BY id
MEASURES classifier() AS trg
ALL ROWS PER MATCH
PATTERN (S (R X R+)?)
DEFINE
R AS sign(R.amount) = prev(sign(R.amount)),
X AS sign(X.amount) = prev(sign(X.amount))
)
What do we do here?
- We order the table by
ID, which is the order in which we want to match events. Easy. - We then specify the values that we want as a result. We want the “MEASURE” trg, which is defined as the classifier, i.e. the literal that we’ll use in the
PATTERNafterwards. Plus we want all the rows from a match. - We then specify a regular expression-like pattern. The pattern is an event “S” for Start, followed optionally by “R” for Repeat, “X” for our special event X, followed by one or more “R” for repeat again. If the whole pattern matches, we get SRXR or SRXRR or SRXRRR, i.e. X will be at the third position of a series of length >= 4
- Finally, we define R and X as being the same thing: The event when
SIGN(AMOUNT)of the current row is the same asSIGN(AMOUNT)of the previous row. We don’t have to define “S”. “S” is just any other row.
This query will magically produce the following output:
| ID | VALUE_DATE | AMOUNT | TRG | |------|------------|---------|-----| | 9997 | 2014-03-18 | + 99.17 | S | | 9981 | 2014-03-16 | - 71.44 | R | | 9979 | 2014-03-16 | - 94.60 | X | | 9977 | 2014-03-16 | - 6.96 | R | | 9971 | 2014-03-15 | - 65.95 | S | | 9964 | 2014-03-15 | + 15.13 | S | | 9962 | 2014-03-15 | + 17.47 | S | | 9960 | 2014-03-15 | + 3.55 | S | | 9959 | 2014-03-14 | - 32.00 | S |
We can see a single “X” in our event stream. Exactly where we had expected it. At the 3rd repetition of an event (same sign) in a series of length > 3.
Boom!
As we don’t really care about “S” and “R” events, let’s just remove them as such:
SELECT
id, value_date, amount,
CASE trg WHEN 'X' THEN 'X' END trg
FROM series
MATCH_RECOGNIZE (
ORDER BY id
MEASURES classifier() AS trg
ALL ROWS PER MATCH
PATTERN (S (R X R+)?)
DEFINE
R AS sign(R.amount) = prev(sign(R.amount)),
X AS sign(X.amount) = prev(sign(X.amount))
)
to produce:
| ID | VALUE_DATE | AMOUNT | TRG | |------|------------|---------|-----| | 9997 | 2014-03-18 | + 99.17 | | | 9981 | 2014-03-16 | - 71.44 | | | 9979 | 2014-03-16 | - 94.60 | X | | 9977 | 2014-03-16 | - 6.96 | | | 9971 | 2014-03-15 | - 65.95 | | | 9964 | 2014-03-15 | + 15.13 | | | 9962 | 2014-03-15 | + 17.47 | | | 9960 | 2014-03-15 | + 3.55 | | | 9959 | 2014-03-14 | - 32.00 | |
Thank you Oracle!
Again, don’t expect me to explain this any better than the excellent Oracle white paper already did, which I strongly recommend reading if you’re using Oracle 12c anyway:
http://www.oracle.com/ocom/groups/public/@otn/documents/webcontent/1965433.pdf
9. Pivoting and Unpivoting
If you’ve read this far, the following will be almost too embarassingly simple:
This is our data, i.e. actors, film titles, and film ratings:
| NAME | TITLE | RATING | |-----------|-----------------|--------| | A. GRANT | ANNIE IDENTITY | G | | A. GRANT | DISCIPLE MOTHER | PG | | A. GRANT | GLORY TRACY | PG-13 | | A. HUDSON | LEGEND JEDI | PG | | A. CRONYN | IRON MOON | PG | | A. CRONYN | LADY STAGE | PG | | B. WALKEN | SIEGE MADRE | R |
This is what we call pivoting:
| NAME | NC-17 | PG | G | PG-13 | R | |-----------|-------|-----|-----|-------|-----| | A. GRANT | 3 | 6 | 5 | 3 | 1 | | A. HUDSON | 12 | 4 | 7 | 9 | 2 | | A. CRONYN | 6 | 9 | 2 | 6 | 4 | | B. WALKEN | 8 | 8 | 4 | 7 | 3 | | B. WILLIS | 5 | 5 | 14 | 3 | 6 | | C. DENCH | 6 | 4 | 5 | 4 | 5 | | C. NEESON | 3 | 8 | 4 | 7 | 3 |
Observe how we kinda grouped by the actors and then “pivoted” the number films per rating each actor played in. Instead of displaying this in a “relational” way, (i.e. each group is a row) we pivoted the whole thing to produce a column per group. We can do this, because we know all the possible groups in advance.
Unpivoting is the opposite, when from the above, we want to get back to the “row per group” representation:
| NAME | RATING | COUNT | |-----------|--------|-------| | A. GRANT | NC-17 | 3 | | A. GRANT | PG | 6 | | A. GRANT | G | 5 | | A. GRANT | PG-13 | 3 | | A. GRANT | R | 6 | | A. HUDSON | NC-17 | 12 | | A. HUDSON | PG | 4 |
It’s actually really easy. This is how we’d do it in PostgreSQL:
SELECT first_name, last_name, count(*) FILTER (WHERE rating = 'NC-17') AS "NC-17", count(*) FILTER (WHERE rating = 'PG' ) AS "PG", count(*) FILTER (WHERE rating = 'G' ) AS "G", count(*) FILTER (WHERE rating = 'PG-13') AS "PG-13", count(*) FILTER (WHERE rating = 'R' ) AS "R" FROM actor AS a JOIN film_actor AS fa USING (actor_id) JOIN film AS f USING (film_id) GROUP BY actor_id
We can append a simple FILTER clause to an aggregate function in order to count only some of the data.
In all other databases, we’d do it like this:
SELECT first_name, last_name, count(CASE rating WHEN 'NC-17' THEN 1 END) AS "NC-17", count(CASE rating WHEN 'PG' THEN 1 END) AS "PG", count(CASE rating WHEN 'G' THEN 1 END) AS "G", count(CASE rating WHEN 'PG-13' THEN 1 END) AS "PG-13", count(CASE rating WHEN 'R' THEN 1 END) AS "R" FROM actor AS a JOIN film_actor AS fa USING (actor_id) JOIN film AS f USING (film_id) GROUP BY actor_id
The nice thing here is that aggregate functions usually only consider non-NULL values, so if we make all the values NULL that are not interesting per aggregation, we’ll get the same result.
Now, if you’re using either SQL Server, or Oracle, you can use the built-in PIVOT or UNPIVOT clauses instead. Again, as with MODEL or MATCH_RECOGNIZE, just append this new keyword after a table and get the same result:
-- PIVOTING
SELECT something, something
FROM some_table
PIVOT (
count(*) FOR rating IN (
'NC-17' AS "NC-17",
'PG' AS "PG",
'G' AS "G",
'PG-13' AS "PG-13",
'R' AS "R"
)
)
-- UNPIVOTING
SELECT something, something
FROM some_table
UNPIVOT (
count FOR rating IN (
"NC-17" AS 'NC-17',
"PG" AS 'PG',
"G" AS 'G',
"PG-13" AS 'PG-13',
"R" AS 'R'
)
)
Easy. Next.
10. Abusing XML and JSON
First off
JSON is just XML with less features and less syntax
Now, everyone knows that XML is awesome. The corollary is thus:
JSON is less awesome
Don’t use JSON.
Now that we’ve settled this, we can safely ignore the ongoing JSON-in-the-database-hype (which most of you will regret in five years anyway), and move on to the final example. How to do XML in the database.
This is what we want to do:
Given the original XML document, we want to parse that document, unnest the comma-separated list of films per actor, and produce a denormalized representation of actors/films in a single relation.
Ready. Set. Go. This is the idea. We have three CTE:
WITH RECURSIVE
x(v) AS (SELECT '...'::xml),
actors(
actor_id, first_name, last_name, films
) AS (...),
films(
actor_id, first_name, last_name,
film_id, film
) AS (...)
SELECT *
FROM films
In the first one, we simply parse the XML. Here with PostgreSQL:
WITH RECURSIVE
x(v) AS (SELECT '
Bud
Spencer
God Forgives... I Don’t, Double Trouble, They Call Him Bulldozer
Terence
Hill
God Forgives... I Don’t, Double Trouble, Lucky Luke
'::xml),
actors(actor_id, first_name, last_name, films) AS (...),
films(actor_id, first_name, last_name, film_id, film) AS (...)
SELECT *
FROM films
Easy.
Then, we do some XPath magic to extract the individual values from the XML structure and put those into columns:
WITH RECURSIVE
x(v) AS (SELECT '...'::xml),
actors(actor_id, first_name, last_name, films) AS (
SELECT
row_number() OVER (),
(xpath('//first-name/text()', t.v))[1]::TEXT,
(xpath('//last-name/text()' , t.v))[1]::TEXT,
(xpath('//films/text()' , t.v))[1]::TEXT
FROM unnest(xpath('//actor', (SELECT v FROM x))) t(v)
),
films(actor_id, first_name, last_name, film_id, film) AS (...)
SELECT *
FROM films
Still easy.
Finally, just a bit of recursive regular expression pattern matching magic, and we’re done!
WITH RECURSIVE
x(v) AS (SELECT '...'::xml),
actors(actor_id, first_name, last_name, films) AS (...),
films(actor_id, first_name, last_name, film_id, film) AS (
SELECT actor_id, first_name, last_name, 1,
regexp_replace(films, ',.+', '')
FROM actors
UNION ALL
SELECT actor_id, a.first_name, a.last_name, f.film_id + 1,
regexp_replace(a.films, '.*' || f.film || ', ?(.*?)(,.+)?', '\1')
FROM films AS f
JOIN actors AS a USING (actor_id)
WHERE a.films NOT LIKE '%' || f.film
)
SELECT *
FROM films
Let’s conclude:

Conclusion
All of what this article has shown was declarative. And relatively easy. Of course, for the fun effect that I’m trying to achieve in this talk, some exaggerated SQL was taken and I expressly called everything “easy”. It’s not at all easy, you have to practice SQL. Like many other languages, but a bit harder because:
- The syntax is a bit awkward from time to time
- Declarative thinking is not easy. At least, it’s very different
But once you get a hang of it, declarative programming with SQL is totally worth it as you can express complex relationships between your data in very very little code by just describing the result you want to get from the database.
Isn’t that awesome?
And if that was a bit over the top, do note that I’m happy to visit your JUG / conference to give this talk (just contact us), or if you want to get really down into the details of these things, we also offer this talk as a public or in-house workshop. Do get in touch! We’re looking forward.
See again the full set of slides here: